
In many cases, a computational chemist calculates the energy change ΔE of an interesting process (e.g., conformational transition or formation of an intermolecular complex), hoping to identify the energetic "components" of distinct physical origin. Contributions to such "energetic decomposition analysis" (EDA) may include:
The EL component may be further divided into static (ES) and induced "polarization" (POL) components [with associated "self-energy" (SE) correction for the energetic penalty at each polarizing center], and post-HF "correlation" (CORR) or other components may be added in more refined treatments. However, the contentious literature of conflicting EDA schemes centers mainly on the magnitude of quantum-mechanical CT vs. quasi-classical EL + EX components in additive decompositions of the form
Although there is widespread agreement on the general form of Eq. (1) and the quantum mechanical integrals contributing to overall ΔE, sharp disagreements persist on how individual integrals should be regrouped for labelling as "EL", "EX", "CT" contributions.
The pioneer EDA formulation of Morokuma and coworkers [1] (MEDA) was initially developed for interacting A, B monomers of a supramolecular A···B complex, but similar schemes were later adopted for torsional interactions of alkyl radicals about a connecting bond [2]. The common assumption of these formulations is that the quasi-classical EL + EX contributions can be evaluated as
Here, ψA, ψB are antisymmetrized determinantal wavefunctions for isolated A, B subunits, placed at equilibrium A···B separation in the Hamiltonian integral. The EL component is commonly evaluated as a classical Coulomb integral between the corresponding electron densities ρA, ρB at the two centers, viz.,
and remaining EX(MEDA), CT(MEDA) components are then determined by difference from Eqs. (1), (2). In particular, the CT component is evaluated as the "remainder" term
independent of how EL(MEDA) is evaluated.
The integral <ψA|H|ψB>eq superficially resembles the perturbative interaction integral between unperturbed ψA, ψB wavefunctions of the non-interacting long-range limit. Indeed, as RAB → ∞, this interpretation is valid and Eqs. (2)-(3) become exact. In the same limit, ψA, ψB are mutually orthogonal and CT(MEDA) vanishes, in accordance with London's long-range perturbation theory [3].
However, at the actual equilibrium separation of the A···B complex, attempted physical justification of Eqs. (2)-(4) in perturbation-theoretic terms is certainly invalid. At any finite equilibrium separation, the supposed "unperturbed wavefunctions" ψA, ψB are nonorthogonal [4]
and no possible physical (Hermitian) "unperturbed Hamiltonian" could underlie such interpretation (because non-degenerate solutions of Hermitian eigenvalue problems are necessarily orthogonal). For H-bonded complexes, equilibrium RAB separations are commonly found to be 0.5-1.0 Ångstrom inside the formal van der Waals contact distance at which exchange-type overlap is expected to increase exponentially, and for torsional interactions the overlap issues are still more severe. MEDA-style components are therefore seen to be inherently dependent on AO overlap (required, e.g., for any non-zero evaluation of CT(MEDA)), exemplifying "overlap-dependent" interpretation (and labeling) of CT.
Why is AO overlap a critical issue for evaluation of CT? As shown in Eq. (4), MEDA evaluation of CT originates not in physical identification of donor-acceptor (filled-unfilled) orbital interactions, but in the overlap-dependent "remainder" of a long-range identity that is applied improperly in the region of significant exchange-type interactions. This contrasts sharply with NBO-based EDA techniques, which are always formulated in the overlap-free domain of NAOs, assuring strict probability conservation and consistent natural charge assignments throughout subsequent hybridization, covalent bond formation, and supramolecular complex formation. Disagreements between MEDA and NBO-based EDA assignments of CT can therefore be traced squarely to disparate handling of AO overlap [5].
The intrinsic ambiguities of overlap-dependent charge assignments strongly affect how electrons are perceived to be distributed between one atomic center or another (as well known, e.g., in the pathologies of Mulliken population analysis). Morokuma-type evaluation of CT is intrinsically tied to ambiguous AO overlap terms that confuse assignments of atomic charge, resulting in profound disagreements over "transfer" between one monomer or the other. Related Ziegler-Rauk, Bickelhaupt-Baerends, BLW, and ALMO-EDA methods [6] handle overlap-density terms in slightly different ways, but all differ sharply from overlap-free NBO methods in this respect.
While NCE, STERIC, and $DEL keywords allow quantitation of NBO-based EL-, EX-, and CT-type energy contributions, they do not account for expected non-additive coupling terms between these components (corresponding to "higher-order effects" in perturbative parlance). Important coupling effects include:
To incorporate such higher-order effects consistently in traditional EDA-style additive components, Glendening and coworkers [7] developed the "Natural Energy Decomposition Analysis" (NEDA) method. The NEDA keyword requires an intricate sequence of interactive calculations between NBO6 and host ESS, and is currently implemented only in GAMESS, FIREFLY (PC-GAMESS), and NWCHEM host systems.
Similar to Eq. (1), NEDA partitions the usual expression for the binding energy ΔE of the A···B complex
into a sum of "electrical" (EL), "core" (CORE), and "charge transfer" (CT) components which may be abbreviated as
All NEDA energy evaluations in Eq. (6) employ the full basis set of the complex, so that ΔE automatically incorporates the full Boys-Bernardi "counterpoise correction" [8] for BSSE.
The key step of NEDA analysis is evaluation of perturbed ("deformed") wavefunctions (ψA(def), ψB(def)) for each monomer as local eigenvectors of the NBO Fock matrix in the respective monomer blocks. (Each monomer wavefunction ψA(def), ψB(def) thereby inherits the overlap-free character of the underlying NAOs.) The antisymmetrized (determinantal) product of perturbed fragment wavefunctions
then defines the starting "localized" (ψ(loc)) wavefunction that underlies evaluation of each NEDA component.
Consistent with its physical description as "delocalization" from each fragment into unfilled orbitals of the other, the charge transfer (CT) component is defined directly as
rather than, as in Eq. (4), a "remainder" term. As usual, the energy difference between ψ(loc) and the perturbed fragment wavefunctions ψA(def), ψB(def) is attributed to a sum of electrostatic (ES), polarization (POL) and exchange (EX) contributions, viz.,
The "deformation" energy (DEF) of forming each perturbed localized ψA(def) from its starting fragment wavefunction ψA is evaluated in a similarly direct manner as
corresponding to combined electric field and quantum mechanical effects experienced by each fragment within the complex.
In accordance with classical electrodynamics, one can employ linear response theory to evaluate the self-energy (SE) correction ("polarization penalty") for each center, thereby expressing the total electrical component as
However, the self-energy must then be removed (subtracted) from the deformation (DEF) penalty to obtain the net repulsive CORE component, viz.,
By combining the definitions for EL [Eq. (12)], CORE [Eq. (13)], and CT [Eq. (9)], one readily verifies that these components satisfy the basic NEDA ansatz, Eq. (7).
In addition to the energies E(ψA), E(ψA(def)), NEDA also calculates the dipole moments (μA, μA(def)) for the wavefunctions ψA, ψA(def) of each fragment. The difference between these two vector quantities is a measure of the induced dipole due to complex formation, which asymptotically reduces to the corresponding classical expression in the long-range limit.
NEDA differs significantly from other NBO keyword options. The "NEDA" keyword is only allowed within a $DEL keylist (not in the usual $NBO keylist) and must always appear with accompanying "END" in keylist-like "NEDA [fragment units] END" form. For the sake of specificity in the tutorial instructions below, we assume that GAMESS is the host ESS program and that the user has some general familiarity with GAMESS keyword groups and syntax.
Full details of "[fragment units]" specification will be described below. However, in the simplest and most common closed-shell application, when the desired NEDA fragments A, B,... are the same as the "molecular units" returned by default NBO analysis, default NEDA analysis could be run merely by appending the following lines to the GAMESS input deck:
$NBO $END $DEL NEDA END $END
For an open-shell species, the corresponding $DEL keylist could be of the form
$DEL ALPHA NEDA END BETA NEDA END $END
again implying that the desired fragments A, B,... are those of default NBO search. (Note however that the program will halt if the molecular units of the alpha spin set are different from those of the beta spin set, so more detailed specification of NEDA fragment units is necessary in this case.) One can also choose to perform NEDA with alternative NAO rather than default NBO basis set, in which case the default "units" are individual atoms rather than bonded molecular units of the NBO search (see below).
NEDA fragment wavefunctions can be evaluated by any $SCF group options available in GAMESS input, including SOSCF, DIIS, damping, and direct energy minimization (DEM) methods to control convergence. As in other $DEL applications, use of symmetry should generally be disabled by setting NOSYM=1 in the GAMESS $CONTRL group and NOPK=1 in the $INTGRL group.
Several options are available for specifying the NEDA fragments, if different from default NBO molecular units. The most commonly useful options are:
$NBO $END $DEL NEDA (1,3) (2,6) (4) (5) END $END
$NBO $END $CHOOSE LONE 2 1 END BOND S 1 3 S 1 4 S 1 5 S 2 6 S 2 7 S 2 8 END $END $DEL NEDA END $END
$NBO $END $DEL NAO NEDA (1,3,4,5) (2,6,7,8) END $END
Other $DEL command keywords can be included as usual in the keylist, including alternative NEDA fragment analyses. Each such NEDA or non-NEDA command will be processed in turn for output display. See Sec. B.5 of the NBO Manual for further information on $DEL keylist syntax.
Here's a sample GAMESS input deck for RHF/4-31G calculation of the water dimer (far too low a theoretical level for current "real world" application):
$CONTRL SCFTYP=RHF RUNTYP=ENERGY COORD=HINT NOSYM=1 $END< $INTGRL NOPK=1 $END $BASIS GBASIS=N31 NGAUSS=4 $END $NBO $END $DEL NEDA END $END $DATA Water dimer...(rhf/4-31g//from Umeyama and Morokuma, JACS 99, 1316 (1977) Cs Oxygen 8.0 LC 0.0000 0.0000 0.0000 + O I Hydrogen 1.0 TCT 0.9560 52.6000 90.0000 + O I J Oxygen 8.0 TCT 2.8800 120.0000 0.0000 + O I J Hydrogen 1.0 TCT 0.9560 105.2000 180.0000 + 3 O J Hydrogen 1.0 TCT 0.9560 105.2000 0.0000 + 3 4 O $END
As shown in the $DEL keylist, NEDA will perform default analysis using the two molecular units (water monomers) of the NBO search.
The first segment of NEDA output is shown below, essentially equivalent to usual $DEL output for deletion of all intermolecular delocalizations between the two units (deletion type 8; cf. Sec. B.5 of the NBO Manual):
NEDA: Natural Energy Decomposition Analysis
Deletion of the NBO Fock matrix elements between orbitals:
1 3 4 7 8 11 12 15 16 17 18 19 20
and orbitals:
2 5 6 9 10 13 14 21 22 23 24 25 26
Orbital occupancies:
Orbital No deletions This deletion Change
------------------------------------------------------------------------------
1. CR ( 1) O 1 1.99982 1.99983 0.00001
2. CR ( 1) O 4 1.99979 1.99980 0.00000
3. LP ( 1) O 1 1.99920 1.99930 0.00010
4. LP ( 2) O 1 1.98029 1.99914 0.01885
5. LP ( 1) O 4 1.99994 2.00000 0.00006
6. LP ( 2) O 4 1.99922 1.99932 0.00010
7. BD ( 1) O 1- H 2 1.99912 1.99942 0.00030
8. BD ( 1) O 1- H 3 1.99912 1.99942 0.00030
9. BD ( 1) O 4- H 5 1.99960 1.99961 0.00000
10. BD ( 1) O 4- H 6 1.99919 1.99943 0.00024
11. BD*( 1) O 1- H 2 0.00032 0.00016 -0.00016
12. BD*( 1) O 1- H 3 0.00032 0.00016 -0.00016
13. BD*( 1) O 4- H 5 0.00027 0.00008 -0.00019
14. BD*( 1) O 4- H 6 0.01827 0.00014 -0.01814
15. RY ( 1) O 1 0.00004 0.00001 -0.00003
16. RY ( 2) O 1 0.00002 0.00000 -0.00002
17. RY ( 3) O 1 0.00001 0.00000 -0.00001
18. RY ( 4) O 1 0.00000 0.00001 0.00001
19. RY ( 1) H 2 0.00124 0.00127 0.00003
20. RY ( 1) H 3 0.00124 0.00127 0.00003
21. RY ( 1) O 4 0.00009 0.00000 -0.00009
22. RY ( 2) O 4 0.00002 0.00000 -0.00002
23. RY ( 3) O 4 0.00001 0.00000 0.00000
24. RY ( 4) O 4 0.00000 0.00000 0.00000
25. RY ( 1) H 5 0.00127 0.00120 -0.00007
26. RY ( 1) H 6 0.00159 0.00042 -0.00117
NEXT STEP: Evaluate the energy of the new density matrix
that has been constructed from the deleted NBO
Fock matrix by doing one SCF cycle.
------------------------------------------------------------------------------
--------------------------
RHF SCF CALCULATION
--------------------------
DENSITY MATRIX CONV= 1.00E-05
ITER EX DEM TOTAL ENERGY E CHANGE DENSITY CHANGE ORB. GRAD
1 0 0 -151.8065596360 -151.8065596360 0.061186977 0.000000000
SCF IS UNCONVERGED, TOO MANY ITERATIONS
TIME TO FORM FOCK OPERATORS= 0.0 SECONDS ( 0.0 SEC/ITER)
TIME TO SOLVE SCF EQUATIONS= 0.0 SECONDS ( 0.0 SEC/ITER)
FINAL RHF ENERGY IS 0.0000000000 AFTER 1 ITERATIONS
...... END OF RHF CALCULATION ......
STEP CPU TIME = 0.15 TOTAL CPU TIME = 0.4 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.5 SECONDS, CPU UTILIZATION IS 93.48%
------------------------------------------------------------------------------
Energy of deletion : -151.806559636
Total SCF energy : -151.827680724
-------------------
Energy change : 0.021121 a.u., 13.254 kcal/mol
------------------------------------------------------------------------------
As shown in the final line, the calculated energy change for this deletion is 13.254 kcal/mol. This corresponds to the variational loss of stabilizing charge-transfer delocalizations, so the CT component is simply the negative of this quantity, viz.,
This $DEL estimate of CT is in sensible qualitative agreement with the corresponding perturbative estimate (ΔE(2) = -15.21 kcal/mol) for the dominant nO(1) → σ*O(4)-H(6) interaction (as usual, ΔE(2) somewhat overestimates the variational $DEL energy change, due to neglect of higher-order coupling terms). From the $DEL occupancy changes, one can also see that localizing the wavefunction back-transfers about 0.018 electrons from NBO 14 (the σ*O(4)-H(6) antibond acceptor) to NBO 8 (the nO(2) lone pair donor), effectively suppressing the leading CT interaction of the dimer.
[Note that the warning message "SCF is unconverged, too many iterations" should be ignored, because the single-pass $DEL evaluation method is based on interrupting SCF iterations after the first cycle to evaluate the energy for the input $DEL-density, not the converged SCF density.]
The next segment of output reports on calculation of the perturbed (ψA(def)) and variationally optimized (ψA) wavefunctions for the first fragment, the H(2)-O(1)-H(3) monomer:
--------------
Fragment 1:
--------------
...... END OF ONE-ELECTRON INTEGRALS ......
STEP CPU TIME = 0.03 TOTAL CPU TIME = 0.5 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.5 SECONDS, CPU UTILIZATION IS 93.88%
--------------------------
RHF SCF CALCULATION
--------------------------
DENSITY MATRIX CONV= 1.00E-05
ITER EX DEM TOTAL ENERGY E CHANGE DENSITY CHANGE ORB. GRAD
1 0 0 -75.8820038771 -75.8820038771 0.051585286 0.000000000
---------------START SECOND ORDER SCF---------------
2 1 0 -75.9081413953 -0.0261375181 0.018452073 0.009561181
3 2 0 -75.9092479375 -0.0011065422 0.009032407 0.003595518
4 3 0 -75.9094058121 -0.0001578747 0.000764754 0.000898516
5 4 0 -75.9094124510 -0.0000066389 0.000263894 0.000128113
6 5 0 -75.9094127399 -0.0000002890 0.000084067 0.000046344
7 6 0 -75.9094127514 -0.0000000114 0.000018443 0.000008466
8 7 0 -75.9094127518 -0.0000000005 0.000003845 0.000002277
9 8 0 -75.9094127518 0.0000000000 0.000001199 0.000000691
-----------------
DENSITY CONVERGED
-----------------
TIME TO FORM FOCK OPERATORS= 0.0 SECONDS ( 0.0 SEC/ITER)
TIME TO SOLVE SCF EQUATIONS= 0.0 SECONDS ( 0.0 SEC/ITER)
FINAL RHF ENERGY IS -75.9094127518 AFTER 9 ITERATIONS
...... END OF RHF CALCULATION ......
STEP CPU TIME = 0.05 TOTAL CPU TIME = 0.5 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.5 SECONDS, CPU UTILIZATION IS 94.44%
...... END OF ONE-ELECTRON INTEGRALS ......
STEP CPU TIME = 0.00 TOTAL CPU TIME = 0.5 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.5 SECONDS, CPU UTILIZATION IS 94.44%
Dipole (def): 2.6394(x), 0.0793(y), 0.0000(z); 2.6406(tot) Debye
Dipole (cp): 2.6541(x), -0.0947(y), 0.0000(z); 2.6557(tot) Debye
Dipole (ind): -0.0146(x), 0.1740(y), 0.0000(z); 0.1747(tot) Debye
The calculated expectation energy of localized ψA(def) (-75.88200 a.u.) is obtained by single-pass SCF evaluation with the localized monomer MOs of the previous step, whereas that of optimized ψA (-75.90941 a.u.) is obtained after complete SCF convergence. Both wavefunctions are calculated in the full dimer basis at the fixed monomer geometry in the complex, thereby incorporating the complete counterpoise (cp) correction for this rather small basis.
The final lines of this segment display the calculated dipole moment for the perturbed (def) and optimized (cp) wavefunctions, showing the relatively small shift (induced "ind" dipole = 0.1747 Debye) from 2.6406 in the isolated monomer to 2.6557 Debye in the presence of the other monomer. In effect, the strict orthogonality required of the two monomer wavefunctions prevents the electron distribution of the donor from significantly penetrating the acceptor.
A similar report then follows for the acceptor fragment H(5)-O(4)-H(6):
--------------
Fragment 2:
--------------
...... END OF ONE-ELECTRON INTEGRALS ......
STEP CPU TIME = 0.04 TOTAL CPU TIME = 0.5 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.6 SECONDS, CPU UTILIZATION IS 96.49%
--------------------------
RHF SCF CALCULATION
--------------------------
DENSITY MATRIX CONV= 1.00E-05
ITER EX DEM TOTAL ENERGY E CHANGE DENSITY CHANGE ORB. GRAD
1 0 0 -75.8962673806 -75.8962673806 0.016278993 0.000000000
---------------START SECOND ORDER SCF---------------
2 1 0 -75.9079696846 -0.0117023040 0.007570847 0.005067234
3 2 0 -75.9083141028 -0.0003444182 0.005463348 0.001684405
4 3 0 -75.9083555888 -0.0000414859 0.001012338 0.000672210
5 4 0 -75.9083571171 -0.0000015284 0.000352290 0.000297195
6 5 0 -75.9083574089 -0.0000002918 0.000092465 0.000043124
7 6 0 -75.9083574187 -0.0000000097 0.000014019 0.000006844
8 7 0 -75.9083574192 -0.0000000005 0.000004722 0.000002775
9 8 0 -75.9083574192 -0.0000000001 0.000000684 0.000000532
-----------------
DENSITY CONVERGED
-----------------
TIME TO FORM FOCK OPERATORS= 0.0 SECONDS ( 0.0 SEC/ITER)
TIME TO SOLVE SCF EQUATIONS= 0.0 SECONDS ( 0.0 SEC/ITER)
FINAL RHF ENERGY IS -75.9083574192 AFTER 9 ITERATIONS
...... END OF RHF CALCULATION ......
STEP CPU TIME = 0.04 TOTAL CPU TIME = 0.6 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.6 SECONDS, CPU UTILIZATION IS 95.16%
...... END OF ONE-ELECTRON INTEGRALS ......
STEP CPU TIME = 0.01 TOTAL CPU TIME = 0.6 ( 0.0 MIN)
TOTAL WALL CLOCK TIME= 0.6 SECONDS, CPU UTILIZATION IS 96.77%
Dipole (def): -0.8286(x), -2.6607(y), 0.0000(z); 2.7867(tot) Debye
Dipole (cp): -1.0045(x), -2.3894(y), 0.0000(z); 2.5919(tot) Debye
Dipole (ind): 0.1759(x), -0.2713(y), 0.0000(z); 0.3234(tot) Debye
In this case, the induced dipole for the acceptor is seen to be rather sizable (0.3234 Debye), reflecting the significant polarization of σO(4)H(6) away from the donor (thereby better exposing σ*O(4)H(6) to nucleophilic attack), as seen in the NBO polarization coefficients. Nevertheless, as will be seen in the energy summary below, such polarization (induction) changes make only secondary contributions to H-bond energy.
The final segment of NEDA output summarizes the final CT, ES, POL, EX component values for the complex, as well as the deformation (DEF) and self-energy (SE) values for each monomer:
Natural Energy Decomposition Analysis (Summary):
Component
Energy(wfn) Energy(wfn) (kcal/mol)
------------------------------------------------------------------------------
H4O2 -151.8276807(scf) -151.8065596(loc) CT = -13.25
ES = -12.24
POL = -3.89
EX = -1.62
1. H2O -75.8820039(def) -75.9094128(cp) DEF(SE) = 17.20( 0.10)
2. H2O -75.8962674(def) -75.9083574(cp) DEF(SE) = 7.59( 1.78)
---------
E = -6.22
Electrical (ES+POL+SE) : -14.25
Charge Transfer (CT) : -13.25
Core (EX+DEF-SE) : 21.29
------------
Total Interaction (E) : -6.22
......END OF NBO ANALYSIS......
As shown in the final lines, the combined electrical (EL: -14.25 kcal/mol), charge transfer (CT: -13.25 kcal/mol), and core (CORE: +21.29 kcal/mol) contributions add up to the calculated total interaction energy, -6.22 kcal/mol.
In this case, CT (-13.25 kcal/mol) and ES (-12.24 kcal/mol) are the largest individual contributors to binding, with POL (-3.89 kcal/mol) playing an important secondary role. These strong attractions are necessary to overcome the strong CORE repulsions (+21.29 kcal/mol) at the equilibrium geometry of H-bonding (far inside van der Waals contact), resulting in the final net H-bond energy of -6.22 kcal/mol.
From the introductory discussion, we should generally expect strong differences between NEDA (overlap-free) and MEDA-type (overlap-dependent) decompositions, and the water dimer proves to be no exception. Through the hidden AO overlap terms [5] that enter the <ψA|H|ψB> integral of Eq. (2), the critical nO(1) → σ*O(4)H(6) CT interaction is largely absorbed into "EL + EX" terms in MEDA-type partitioning. CT(MEDA) is then obtained [Eq. (4)] as a feeble "remainder" term, evaluated by Umeyama and Morokuma [1] as CT(MEDA) = -2.1 kcal/mol for RHF/4-31G water dimer (in slightly different geometry).
The near order of magnitude disagreement between what NEDA vs. MEDA partisans consider to be the accurately evaluated "CT" naturally inspires impassioned debate! (The "CT vs. electrostatics" debate in the H-bond case is mirrored by corresponding "CT vs. sterics" debate in the rotation barrier case.) Still greater disagreements separate both methods from the "Intermolecular Perturbation Theory" of Stone and coworkers [9]. According to the latter, CT is not merely of secondary importance, but "ill-defined" and "part of the induction (polarization)" component that "vanishes in the limit of a complete basis" [10].
Despite such points of disagreement with older methods, one can see that NEDA clearly recognizes the importance of EL interactions. Indeed, from NEDA results presented above, one might conclude superficially that the largest contributions to H-bonding (ES + POL + SE: -14.25 kcal/mol) are "electrical" in nature, consistent with the presumption expressed in many textbooks. However, from NCE analysis or similar considerations, one can judge that much of the quasi-classical EL interaction is CT-induced, amplified by the deep inter-penetration of van der Waals radii that only resonance-type CT interactions could enable.
Geometry optimization with deletions can be performed more straightforwardly with Gaussian than with GAMESS. [Such optimizations are possible with GAMESS (see the deletions tutorial for sample input) but require the use of RUNTYP=TRUDGE and Hildebrandt-style coordinate input.] Below is a sample Gaussian input file for performing $DEL-type optimization of the water dimer, using constrained monomer geometries. NEDA is not implemented in Gaussian, so the calculation instead "zeroes delocalizations" between the two monomers in the $DEL keylist. The zeroing of delocalizations between monomers is effectively equivalent to the CT localization of NEDA.
#rhf/4-31g pop=nbo6del opt nosymm Water dimer ...(rhf/4-31g//from Umeyana and Mokokuma, JACS 99, 1316 (1977)) CT-deleted structure: E($DEL) = -151.8222285 (dE = -4.36 kcal/mol) 0 1 O H 1 0.956 H 1 0.956 2 105.2 O 1 rhb 2 a214 3 d3214 H 4 0.956 1 a145 2 d2145 H 4 0.956 5 105.2 1 d1546 rhb 2.88 a214 107.68 d3214 114.64 a145 105.20 d2145 123.52 d1546 0.00 $nbo print=0 nbosum $end $del zero 2 deloc from 1 to 2 from 2 to 1 $end
[Note that such $DEL-type optimizations are performed by non-analytic derivative methods that are quite time-consuming, hence restricted to a limited number of optimization variables in practical applications.]
The results are shown below in graphical comparisons of the Umeyama-Morokuma H-bonded complex (upper) with the no-CT counterpart (lower). From visual comparison, one can see that the no-CT complex differs strongly in both radial and angular characteristics from the actual H-bonded dimer. The no-CT structure reverts to the C2v-symmetric structure expected for a classical "dipole-dipole complex", with no tendency toward linear or near-linear O···H-O alignment. One can also see that H2O···H2O separation increases by more than 0.3 Å to approximate van der Waals contact distance.

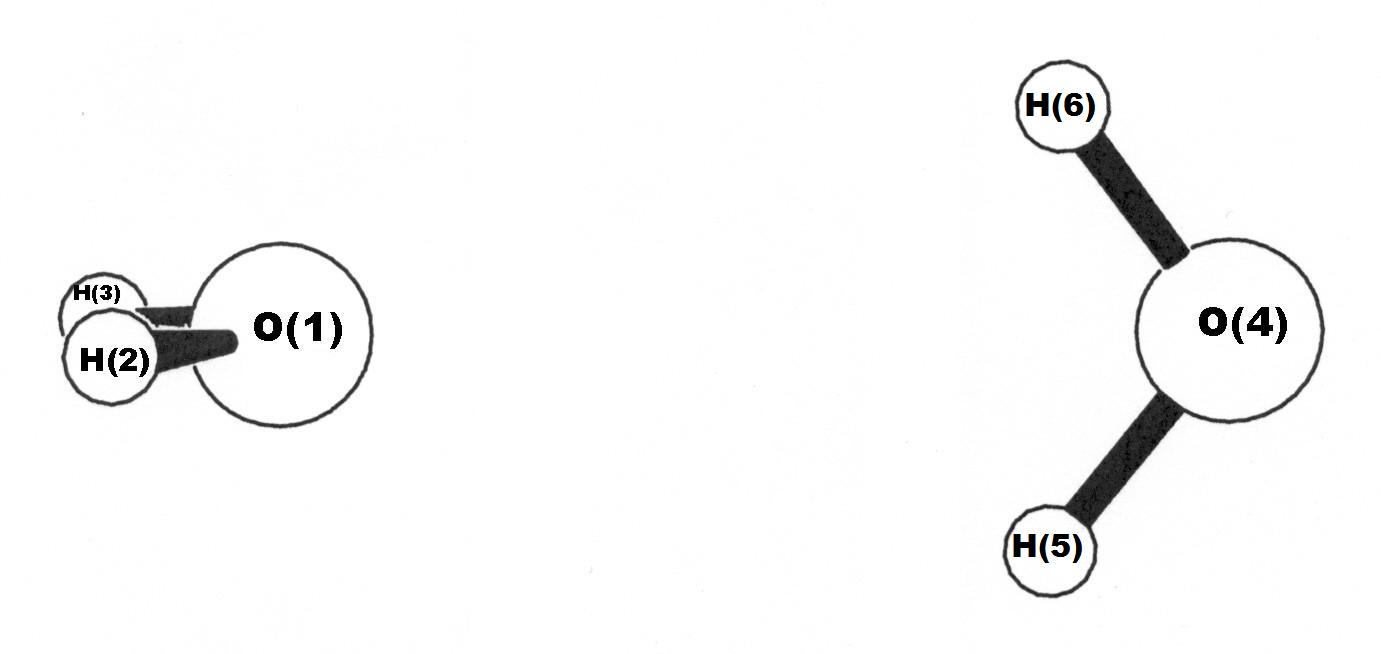
Consistent with RO···O elongation, the net binding energy of the no-CT complex weakens by about 3.4 kcal/mol, to less than half the value of realistic H-bonding. Qualitatively similar differences between the geometry and energetics of full vs. no-CT complexes persist at all higher levels of theory.
At the (unphysical) no-CT geometry, the neglected CT interaction energy (ca. 0.001% of Etotal) is virtually negligible, and only the EL + CORE components remain to exert significant forces on molecular geometry. Although EL attraction appeared only slightly less important than CT in realistic H-bond geometry, the $DEL calculations show clearly that electrostatic forces alone are unable to bring the monomers to the characteristic short distances, near-linear O···H-O alignments, and robust binding energies of authentic H-bond complexes. The resonance-type CT interaction is thereby identified as the unique "smoking gun" necessary to transform feeble dipole-dipole complexes to recognizable H-bonded species. Similar results are obtained [11] across the entire gamut of H-bond energies and types.
[1] K. Kitaura and K. Morokuma, Int. J. Quantum Chem. 10, 325 (1976); H. Umeyama and K. Morokuma, J. Am. Chem. Soc. 99, 1316 (1977); K. Morokuma, Acc. Chem. Res. 10, 294 (1977); K. Morokuma and K. Kitaura, in H. Ratajczak, W. J. Orville-Thomas (eds.), Molecular Interactions (John Wiley, New York, 1980), Vol. 1, pp. 21-66.
[2] K. Morokuma and H. Umeyama, Chem. Phys. Lett. 49, 333 (1977); F. M. Bickelhaupt and E. J. Baerends, Angew. Chem. Int. Ed. 42, 4183 (2003).
[3] F. London, Z. Physik. Chem. B11, 222 (1930); R. Eisenschitz and F. London, Z. Phys. 60, 491 (1930); F. London, Trans. Faraday Soc. 33, 8 (1937); cf. F. Weinhold and C. R. Landis, Valency and Bonding (Cambridge U. Press, New York, 2005), p. 585ff.
[4] It may be questioned how ψA, ψB can be nonorthogonal when they are expanded in AOs on completely disjoint sets of atoms. The answer is that basis AOs on one atom commonly have overlap with AOs on all other atoms at finite separation, so electron density associated with AO-overlap regions cannot be uniquely assigned as being either "on A" or "on B". For further details on the relationship of nonorthogonal AOs to orthonormal NAOs, see the "NAOs in the AO basis" sample output from the MATRIX keyword.
[5] C. T. Corcoran and F. Weinhold, J. Chem. Phys. 72, 2866 (1980); A. E. Reed, L. A. Curtiss, and F. Weinhold, Chem. Rev. 88, 899 (1988); F. Weinhold and J. E. Carpenter, J. Mol. Struct. (Theochem) 165, 189 (1988); F. Weinhold, Angew. Chem. Int. Ed. 42, 4188 (2003).
[6]
Ziegler-Rauk: T. Ziegler and A. Rauk, Inorg. Chem.18, 1558 (1979);
Bickelhaupt-Baerends: F. M. Bickelhaupt and E. J. Baerends,
Rev. Comput. Chem. 15, 1 (2000);
C. Esterhuysen and G. Frenking, Theor. Chem. Acc. 111, 381 (2004);
BLW: Y. Mo and S. D. Peyerimhoff, J. Chem. Phys. 112, 5530 (2000);
Y.Mo, L. Song, and Y. Lin, J. Phys. Chem. A 111, 8291 (2007);
K Nakashima, X. Zhang, M. Xiang, Y. Lin, M. Lin, and Y. Mo,
J. Theo. Chem. Comput. 7, 639 (2008);
ALMO-EDA: R. Z. Khaliullin, R. Lochan, E. Cobar, A. T. Bell, and
M. Head-Gordon, J. Phys. Chem. A 111, 8753 (2007);
R. Z. Khaliullin, A. T. Bell, and M.Head-Gordon, Chem. Eur. J.
15, 851 (2008).
[7] E. D. Glendening and A. Streitwieser Jr., J. Chem. Phys. 100, 2900 (1994); G. K. Schenter and E. D. Glendening, J. Phys. Chem. 100, 17152 (1996); E. D. Glendening, J. Am. Chem.Soc. 118, 2473 (1996).
[8] S. F. Boys and F. Bernardi, Mol. Phys. 19, 553 (1970).
[9] I. C. Hayes and A. J. Stone, Mol. Phys. 53, 69 (1984); A. D. Buckingham, P. W. Fowler, and A. J. Stone, Int. Rev. Phys. Chem. 5, 107 (1986), and refs. therein.
[10] A. J. Stone, Chem. Phys. Lett. 211, 101 (1993).
[11] A. E. Reed, F. Weinhold, L. A. Curtiss, and D. J. Pochatko, J. Chem. Phys. 84, 5687 (1985); F. Weinhold and C. R. Landis, Valency and Bonding (Cambridge U. Press, New York, 2005), Sec. 5.2.