
When interfaced to Gaussian or GAMESS, the NBO program makes it possible to determine the energetic effect of deleting certain NBOs, groups of NBOs, or specific NBO donor-acceptor interactions. This is done by including (following the main $NBO keylist) a special "deletions" $DEL keylist of the form
[For Gaussian, the POP=NBO6DEL keyword (for Rev D) or POP=NBODEL keyword (for pre-Rev D) must also be included on the route card.]
The NBO Manual (Section B.5) describes nine deletion types (each with specific keyword syntax) that can be used to select specific classes of intra- or intermolecular Fock matrix elements for deletion. When combined with geometry optimization, the $DEL keylist also makes it possible to determine the structural consequences of specific NBO donor-acceptor interactions as the difference between the original fully-optimized geometry and the $DEL-optimized geometry.
In this Tutorial we employ $DEL keyword options to illustrate how simple chemical questions may be addressed in the case of a configurational energy difference.
1,2-difluoroethene exists in cis and trans isomers:


Of the two, the trans isomer is expected to be significantly more stable, on the basis of steric and electrostatic factors, because the two bulky F atoms and the repelling negative charges of the two CF bond dipoles are maximally separated in this configuration. However, the cis isomer is actually found to be very similar in energy. For example, for a simple RHF/6-31G* model with idealized trigonal geometry (RCF = 1.33°, RCC = 1.34°, RCH = 1.08°) the calculated energies are
corresponding to only a slight energy difference favoring the trans isomer.
The model RHF calculation exhibits the near-equivalence of cis and trans configurational energies but does not help us to understand why the cis configuration is so competitive. In this Tutorial we show how to address such questions by using $DEL keylists to investigate the effect of specific NBO donor-acceptor interactions on the isomeric energy difference.
The role of electronic delocalization can be quantitatively assessed by deleting all non-Lewis NBOs from the basis set with the LEWIS keyword
The resulting "natural Lewis structure" wavefunction is perfectly localized, with all Lewis-type NBOs doubly occupied. By the variational principle, the Lewis-type wavefunction has an energy E(L) that is higher than the original energy E(full). The net energy difference E(NL)
gives the stabilizing effect of the delocalizing (non-Lewis) contributions.
For the cis isomer, the sample Gaussian input file
# rhf/6-31g* pop=nbo6del nosymm cis-1,2-difluoroethene...rhf/6-31g*//idealized geometry 0 1 C C 1 1.34 F 1 1.33 2 120. F 2 1.33 1 120. 3 0. 0 H 1 1.08 2 120. 3 180. 0 H 2 1.08 1 120. 4 180. 0 $nbo $end $del lewis $end
leads to the $DEL output shown below. The first output segment identifies the type of deletion ("LEWIS: Delete all non-Lewis NBOs") and lists the 48 antibond and Rydberg NBOs (17-64) that are deleted:
LEWIS: Delete all non-Lewis NBOs Deletion of the following orbitals from the NBO Fock matrix: 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
The next segment lists the NBOs with their original occupancies ("No deletions") and current occupancies ("This deletion"), together with the net change in each:
Orbital occupancies:
Orbital No deletions This deletion Change
------------------------------------------------------------------------------
1. CR ( 1) C 1 1.99872 2.00000 0.00128
2. CR ( 1) C 2 1.99872 2.00000 0.00128
3. CR ( 1) F 3 1.99994 2.00000 0.00006
4. CR ( 1) F 4 1.99994 2.00000 0.00006
5. LP ( 1) F 3 1.99225 2.00000 0.00775
6. LP ( 2) F 3 1.97329 2.00000 0.02671
7. LP ( 3) F 3 1.94905 2.00000 0.05095
8. LP ( 1) F 4 1.99225 2.00000 0.00775
9. LP ( 2) F 4 1.97329 2.00000 0.02671
10. LP ( 3) F 4 1.94905 2.00000 0.05095
11. BD ( 1) C 1- C 2 1.99758 2.00000 0.00242
12. BD ( 2) C 1- C 2 1.99676 2.00000 0.00324
13. BD ( 1) C 1- F 3 1.99680 2.00000 0.00320
14. BD ( 1) C 1- H 5 1.98730 2.00000 0.01270
15. BD ( 1) C 2- F 4 1.99680 2.00000 0.00320
16. BD ( 1) C 2- H 6 1.98730 2.00000 0.01270
17. BD*( 1) C 1- C 2 0.02163 0.00000 -0.02163
18. BD*( 2) C 1- C 2 0.09741 0.00000 -0.09741
19. BD*( 1) C 1- F 3 0.00987 0.00000 -0.00987
20. BD*( 1) C 1- H 5 0.01756 0.00000 -0.01756
21. BD*( 1) C 2- F 4 0.00987 0.00000 -0.00987
22. BD*( 1) C 2- H 6 0.01756 0.00000 -0.01756
23. RY ( 1) C 1 0.00612 0.00000 -0.00612
24. RY ( 2) C 1 0.00453 0.00000 -0.00453
25. RY ( 3) C 1 0.00198 0.00000 -0.00198
26. RY ( 4) C 1 0.00131 0.00000 -0.00131
27. RY ( 5) C 1 0.00026 0.00000 -0.00026
28. RY ( 6) C 1 0.00017 0.00000 -0.00017
29. RY ( 7) C 1 0.00008 0.00000 -0.00008
30. RY ( 8) C 1 0.00001 0.00000 -0.00001
31. RY ( 9) C 1 0.00000 0.00000 0.00000
32. RY (10) C 1 0.00000 0.00000 0.00000
33. RY ( 1) C 2 0.00612 0.00000 -0.00612
34. RY ( 2) C 2 0.00453 0.00000 -0.00453
35. RY ( 3) C 2 0.00198 0.00000 -0.00198
36. RY ( 4) C 2 0.00131 0.00000 -0.00131
37. RY ( 5) C 2 0.00026 0.00000 -0.00026
38. RY ( 6) C 2 0.00017 0.00000 -0.00017
39. RY ( 7) C 2 0.00008 0.00000 -0.00008
40. RY ( 8) C 2 0.00001 0.00000 -0.00001
41. RY ( 9) C 2 0.00000 0.00000 0.00000
42. RY (10) C 2 0.00000 0.00000 0.00000
43. RY ( 1) F 3 0.00171 0.00000 -0.00171
44. RY ( 2) F 3 0.00159 0.00000 -0.00159
45. RY ( 3) F 3 0.00007 0.00000 -0.00007
46. RY ( 4) F 3 0.00004 0.00000 -0.00004
47. RY ( 5) F 3 0.00002 0.00000 -0.00002
48. RY ( 6) F 3 0.00001 0.00000 -0.00001
49. RY ( 7) F 3 0.00000 0.00000 0.00000
50. RY ( 8) F 3 0.00000 0.00000 0.00000
51. RY ( 9) F 3 0.00000 0.00000 0.00000
52. RY (10) F 3 0.00000 0.00000 0.00000
53. RY ( 1) F 4 0.00171 0.00000 -0.00171
54. RY ( 2) F 4 0.00159 0.00000 -0.00159
55. RY ( 3) F 4 0.00007 0.00000 -0.00007
56. RY ( 4) F 4 0.00004 0.00000 -0.00004
57. RY ( 5) F 4 0.00002 0.00000 -0.00002
58. RY ( 6) F 4 0.00001 0.00000 -0.00001
59. RY ( 7) F 4 0.00000 0.00000 0.00000
60. RY ( 8) F 4 0.00000 0.00000 0.00000
61. RY ( 9) F 4 0.00000 0.00000 0.00000
62. RY (10) F 4 0.00000 0.00000 0.00000
63. RY ( 1) H 5 0.00061 0.00000 -0.00061
64. RY ( 1) H 6 0.00061 0.00000 -0.00061
Note that this deletion has resulted in all Lewis-type NBOs (1-16) becoming doubly occupied and all remaining non-Lewis-type NBOs (17-64) becoming empty, the idealized Lewis structure limit.
The next output segment displays the calculated energy of the deletion and the energy change (in atomic units and kcal/mol):
NEXT STEP: Perform one SCF cycle to evaluate the energy of the new density
matrix constructed from the deleted NBO Fock matrix.
------------------------------------------------------------------------------
.
.
.
Requested convergence on RMS density matrix=1.00D-08 within 1 cycles.
Requested convergence on MAX density matrix=1.00D-06.
Requested convergence on energy=1.00D-06.
No special actions if energy rises.
Fock symm off for IB=2 I1= 1 I= 25 J= 14 Cut=1.00D-07 Err=3.63D-02
Fock matrix is not symmetric: symmetry in diagonalization turned off.
>>>>>>>>>> Convergence criterion not met.
SCF Done: E(RHF) = -275.461162154 A.U. after 2 cycles
NFock= 1 Conv=0.92D-02 -V/T= 2.0040
.
.
.
------------------------------------------------------------------------------
Energy of deletion : -275.461162154
Total SCF energy : -275.717263936
-------------------
Energy change : 0.256102 a.u., 160.706 kcal/mol
------------------------------------------------------------------------------
[Note that the Gaussian program always prints a "Convergence criterion not met" warning message, because the deleted density does not exactly match the starting density in the one-pass SCF evaluator method used by $DEL. This message can be safely ignored. For the LEWIS case, the energy of deletion is a strict variational expectation value of the natural Lewis structure wavefunction, but for other deletions a slight variational inconsistency is incurred due to the slight difference between the deleted density distribution and the final density from which the converged Fock operator was constructed.]
[Also note that the "nosymm" keyword is added to the route card of the Gaussian input file for deletions calculation to override the use of symmetry in the SCF energy evaluation. This keyword can be safely removed if the deletions to be performed ensure that the deleted density retains the symmetry of the fully delocalized SCF density. In fact, the Lewis deletions described here do preserve symmetry, so "nosymm" could be discarded. However, several of the deletions described below do not preserve symmetry. If uncertain, include "nosymm" on the Gaussian route card. Additional comments on symmetry can be found in Section B.5 of the NBO Manual.]
From the above output, we recognize that
Similarly, from the $DEL output for the trans isomer, we obtain
From these values we find
Thus, the localized E(L) contribution favors the trans configuration by >3 kcal/mol, in accordance with the expected steric and electrostatic differences. However, the small delocalization contribution is seen to strongly favor the cis isomer by a similar amount, leading to nearly equal total energies for the two isomers. The surprising stability of the cis isomer can therefore be attributed to the electronic delocalization energy E(NL).
To further dissect E(NL) into specific donor-acceptor interactions, we can consider more selective $DEL keylists of the form
$DEL delete n elements d1 a1 d2 a2 . . . dn an $END
where each di is the number of a Lewis-type donor NBO and ai is the number of a non-Lewis-type acceptor NBO. For example, the possible vicinal hyperconjugative delocalizations between the CF bond (NBO 13) and CH bond (NBO 14) on C(1) with the CF antibond (NBO 21) and CH antibond (NBO 22) on C(2) could be specified with
$DEL delete 4 elements 13 21 13 22 14 21 14 22 $END
By such exploratory deletions, one can verify that donor-acceptor interactions involving the Rydberg-type (RY) NBOs 23-64 have negligible effect on the cis/trans energy difference. Similarly, interactions involving the acceptor antibond (BD*) NBOs 17-22 are only significant when paired with vicinal donor bond (BD) NBOs on the opposite carbon atom.
The most important contributions to the cis-trans energy difference are found to be the two equivalent vicinal interactions involving CH bonds as donors (NBOs 14,16) and CF* antibonds as acceptors (NBOs 19,21). The 14-21 interaction, e.g., can be deleted with the $DEL keylist
$DEL delete 1 element 14 21 $END
The deletion energy for each such CH-CF* interaction is found to be 5.97 kcal/mol in the cis isomer but only 1.19 kcal/mol in the trans isomer, thus contributing strongly to stabilizing the cis isomer. (The calculated deletion energies agree sensibly with the corresponding 2nd-order perturbative estimates of 6.86 and 1.40 kcal/mol.)
Why do vicinal CH-CF* interactions favor the cis isomer? Each such CH-CF* interaction is antiperiplanar in the cis isomer, but synperiplanar in the trans isomer. As simple NBO overlap diagrams make clear, this delocalizing interaction is considerably stronger in the anti arrangement than in the syn.
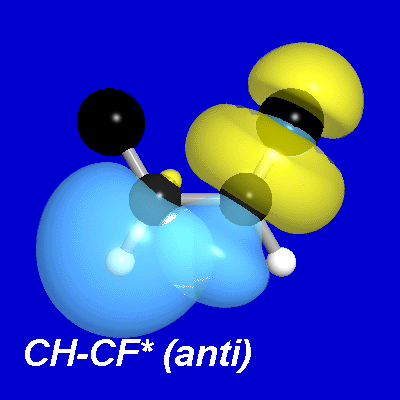
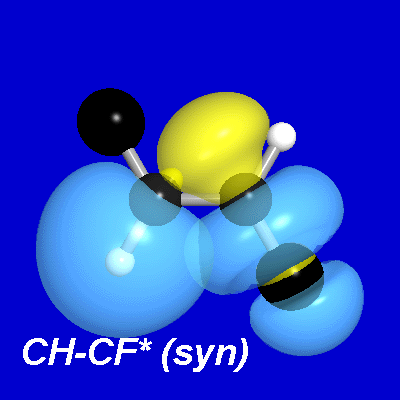
Thus, the cis isomer benefits from two strong antiperiplanar CH-CF* delocalizations, whereas the trans isomer has none. [There is evidently a similar syn/anti difference between CH-CH* interactions that favors the trans isomer, but the CH-CF* interactions are the more important due to the greater acceptor strength of the CF* antibond.] We can therefore conclude that vicinal CH-CF* donor-acceptor interactions are most responsible for stabilizing the cis isomer.
From the NBO overlap diagrams shown above, we can visualize how slight distortions of geometry might further strengthen the donor-acceptor interactions. In the cis isomer, for example, opening up the C-C-F angle or closing down the C-C-H angle will both increase the favorable overlap between the backside lobe of the CF* antibond and the shoulder of the CH bond to allow stronger delocalization and stabilization, as will shortening the central C-C bond. Such distortions would naturally be opposed by the skeletal bonding framework, as the bonding hybrids strive to maintain optimal orientations and separations for strong covalent bonding. Given the weakness of hyperconjugative donor-acceptor delocalizations compared to covalent bonding interactions, we expect that the hyperconjugative effects on molecular geometry are small but detectable (perhaps a few degrees or a few hundredths of an Angstrom). How can we quantitate these hyperconjugative distortions?
A $DEL keylist combined with geometry optimization allows one to determine what the optimal geometry would be in the absence of a particular hyperconjugative interaction. As a simple example, let us consider how the geometry of difluoroethene would be altered if the two CF* antibonds were not present, so that no hyperconjugative delocalizations involving these orbitals were possible. We can address this question by re-optimizing the geometry with the two CF* antibonds (NBOs 19,21) deleted. The G09 input file to perform such a $DEL-optimization for the cis isomer is shown below. (The corresponding input file for GAMESS is given at the end of this tutorial.)
# rhf/6-31g* pop=nbo6del nosymm opt Geometry optimization of cis-1,2-difluoroethene (no CF*s) 0 1 C C 1 CC F 1 CF 2 CCF F 2 CF 1 CCF 3 0. 0 H 1 CH 2 CCH 3 180. 0 H 2 CH 1 CCH 4 180. 0 CC 1.34 CF 1.33 CH 1.08 CCF 120. CCH 120. $nbo $end $choose lone 3 3 4 3 end bond d 1 2 s 1 3 s 1 5 s 2 4 s 2 6 end $end $del delete 2 orbitals 19 21 $end
In this job, the Gaussian geometry optimizer searches for an equilibrium structure on the E($DEL) surface, which differs from the E(full) surface by deletion of contributions from NBOs 19,21. Removing the POP=NBO6DEL keyword and repeating the optimization yields the usual full-basis optimized structure for comparison. Some bond angles and distances for the E(full) and E($DEL) optimized geometries are shown in the table below:
| Geometry Parameter | full | $DEL | diff | |
|---|---|---|---|---|
| bond length (Å) | C-C | 1.307 | 1.342 | -0.035 |
| C-F | 1.324 | 1.308 | +0.016 | |
| C-H | 1.070 | 1.070 | 0.000 | |
| bond angle (°) | C-C-F | 122.6 | 117.9 | +4.7 |
| C-C-H | 123.0 | 127.8 | -4.8 | |
From these comparisons one can see that delocalizations into the CF* antibonds have three primary effects on molecular geometry: (i) significant shortening (by 0.035 A) of the central C-C bond length; (ii) significant opening (by 4.7 degrees) of the C-C-F bond angle; (iii) significant closing (by 4.8 degrees) of the C-C-H bond angle. As noted above, all three of these changes are expected to enhance CH-CF* delocalization by strengthening donor-acceptor overlap.
Similar optimizations of the trans isomer reveal that CF* delocalizations shorten the C-C bond length but have comparatively limited influence on the C-C-F and C-C-H bond angles:
| Geometry Parameter | full | $DEL | diff | |
|---|---|---|---|---|
| bond length (Å) | C-C | 1.307 | 1.340 | -0.033 |
| C-F | 1.329 | 1.308 | +0.021 | |
| C-H | 1.070 | 1.072 | -0.002 | |
| bond angle (°) | C-C-F | 120.2 | 121.0 | -0.8 |
| C-C-H | 125.3 | 124.5 | +0.8 | |
[Note that we recommend using the directed NBO search ($CHOOSE input) when performing geometry optimizations with deletions. These optimizations are based on numerical gradients, and thereby sample a large number of geometries as E($DEL) is minimized. $CHOOSE input ensures that NBO uses the same Lewis structure at each geometry. Because the orbital numbers used to specify the deletion are tied directly to a particular Lewis structure, changes in the Lewis structure from geometry to geometry are bound to confuse the optimizer. $CHOOSE input is described in Section B.4 of the NBO Manual.]
The following is the corresponding input file for GAMESS for 1,2-cis-difluoroethene.
$contrl scftyp=rhf runtyp=trudge coord=hint $end $basis gbasis=n31 ngauss=6 ndfunc=1 $end $trudge optmiz=geometry npar=5 iex(1)=11,21,22,31,32 $end $trurst tolf=0.0001 tolr=0.001 fnoise=0.00001 $end $nbo $end $choose lone 3 3 4 3 end bond d 1 2 s 1 3 s 1 5 s 2 4 s 2 6 end $end $del delete 2 orbitals 19 21 $end $data Geometry optimization of cis-1,2-difluoroethene (no CF*s) Cnv 2 C 6. LC 0.67 0.00 0.00 + O I F 9. TCT 1.33 120.00 0.00 + 1 O K H 1. TCT 1.08 120.00 180.00 + 1 O K $end
Note that the calculation uses GAMESS' TRUDGE numerical optimizer and that the geometry must be specified in Hildebrandt (coord=hint) internal coordinates. See the GAMESS manual for information on runtyp=trudge, coord=hint, and the $trudge and $trurst groups. GAMESS optimizes the cis isomer to the same $DEL geometry described above.