NRT Transition State Analysis ($NRTSTR Keylist)

Introduction to NRT Analysis of Transition State Structures

A chemical reaction can be described as a rearrangement of the chemical bonding pattern between atoms. To characterize a chemical reaction at the electronic level along a chosen reaction coordinate s, one must therefore describe the continuous electronic redistribution from the reactant-like to product-like bonding pattern. For this purpose no single NBO Lewis structure is adequate.

Instead, we can envision the evolving reaction system as a resonance hybrid of the competing R (reactant) and P (product) bonding patterns, corresponding to the Natural Resonance Theory description. The NRT resonance weightings wR(s), wP(s) are expected to vary continuously along the reaction coordinate from the initial reactant species

s = 0 (equilibrium reactant): wR ~ 1, wP ~ 0

to the final product species,

s = 1 (equilibrium product): wR ~ 0, wP ~ 1

At intermediate s = sTS the system passes through a strongly mixed transition state (TS) species that is expected to have nearly equal weightings of reactant-like and product-like character

s = sTS: wR ~ wP ~ 1/2

Energetically, the TS species often corresponds to a topological saddle point on the potential energy surface, representing the highest point of the energetic barrier that separates the equilibrium reactant and product species

However, the criterion for a species having NRT resonance weightings "half-way" between idealized reactant and product forms

wR(sNTS) = wP(sNTS)

can be used to define the natural transition state (NTS) even in barrierless cases where the usual topological criterion is inapplicable (i.e., bond dissociation).

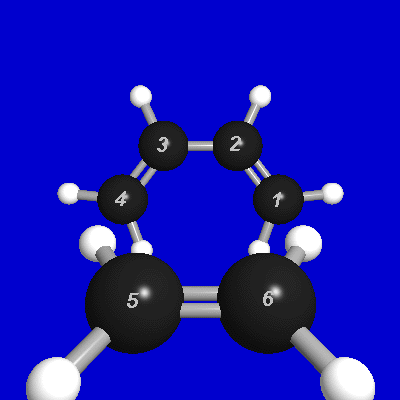
In the present tutorial we shall illustrate the NRT description of a simple model Diels-Alder reaction between ethylene and cis-butadiene to give cyclohexene:

===>

We examine selected NBO bonding indices of this reaction as it evolves along the reaction coordinate between reactant (ethylene + butadiene; s = 0) and product (cyclohexene; s = 1) limits.

Selection of NRT Reference Structures with the $NRTSTR Keylist in pre-NBO7 versions

In the transition state region, both R and P bonding patterns are expected to serve as "reference structures" in the 2-reference NRT expansion. However, in either the R or P equilibrium region the system is expected to be well described by a single-reference NRT expansion, with only a small "secondary" contribution from the opposite resonance structure (i.e., from wP in the R region or wR in the P region). In pre-NBO7 versions, the secondary contributions were treated in a more approximate manner (requiring only diagonal density matrix elements) to conserve storage. However, in order to avoid the discontinuities that accompany promotion of a structure from secondary to reference status, it was necessary to specify that both the R and P structures be chosen as reference structures at every point. This was done with the $NRTSTR keylist, which overrides default selection of reference structures and insures numerical continuity of NRT weightings and bond orders along the entire reaction coordinate.

The form of the $NRTSTR keylist closely parallels that of the $CHOOSE keylist. However, each resonance structure specification is enclosed within delimiting STR ... END keywords

     STR 
       (resonance structure specification)
     END

and these structure specifications are enclosed within delimiting $NRTSTR and $END keywords in the general form

     $NRTSTR
       STR 
         (first structure)
       END
       STR 
         (second structure)
       END
       .
       .
       STR 
         (last structure)
       END
     $END

Although not obligatory in all program systems, it is good practice (as shown above) to put each STR or END keyword, as well as the overall $STR and $END keylist delimiters, on separate lines. The $NRTLST keylist should follow the main $NBO keylist. All $NRTLST input is case-insensitive, and any line of input can be terminated with an exclamation point (!) and ensuing comments, which are ignored by the program.

Preparing the $NRTSTR Keylist for the Model Diels-Alder Reaction

With the atom numbering for the model ethylene + butadiene reactant species shown above, the R structure has the bond elements

     STR           !reactant (ethylene + butadiene) structure
       bond
         d 1 2   s 2 3   d 3 4   d 5 6                 !CC bonds
         s 1 7   s 1 8   s 2 9   s 3 10  s 4 11        !CH bonds
         s 4 12  s 5 13  s 5 14  s 6 15  s 6 16        !CH bonds
       end
     END

Similarly, the P structure is specified by

     STR           !product (cyclohexene) structure
       bond
         s 1 2   d 2 3   s 3 4   s 4 5   s 5 6   s 1 6 !CC bonds
         s 1 7   s 1 8   s 2 9   s 3 10  s 4 11        !CH bonds
         s 4 12  s 5 13  s 5 14  s 6 15  s 6 16        !CH bonds
       end
     END

(As in a $CHOOSE keylist, the entry "d 1 2" in the R structure signifies that there is a double bond between C1 and C2, while the corresponding entry "s 1 2" in the P structure signifies a single bond between these atoms.)

The complete $NRTSTR keylist includes both these structures, as illustrated in the following Gaussian input file for the TS structure (B3LYP/6-31+G* level):

   #B3LYP/6-31+G* Pop=NBORead

   Diels-Alder transition state, 2-reference structure NRT

   0 1
     6     -0.323690    0.515064    1.385000
     6      0.749331    1.138824    0.686505
     6      0.749331    1.138824   -0.686505
     6     -0.323690    0.515064   -1.385000
     6     -0.323690   -1.482636   -0.727700
     6     -0.323690   -1.482636    0.727700
     1     -1.339593    0.697162    1.042309
     1     -0.255039    0.452775    2.470449
     1      1.640684    1.441398    1.233700
     1      1.640684    1.441398   -1.233700
     1     -1.339593    0.697162   -1.042309
     1     -0.255039    0.452775   -2.470449
     1     -1.238374   -1.802237   -1.223944
     1      0.580613   -1.816610   -1.229528
     1     -1.238374   -1.802237    1.223944
     1      0.580613   -1.816610    1.229528

   $NBO file=TS NRT $END
   $NRTSTR
     STR           !reactant (ethylene + butadiene) structure
       bond
         d 1 2   s 2 3   d 3 4   d 5 6                 !CC bonds
         s 1 7   s 1 8   s 2 9   s 3 10  s 4 11        !CH bonds
         s 4 12  s 5 13  s 5 14  s 6 15  s 6 16        !CH bonds
       end
     END
     STR           !product (cyclohexene) structure
     STR           !product (cyclohexene) structure
       bond
         s 1 2   d 2 3   s 3 4   s 4 5   s 5 6   s 1 6 !CC bonds
         s 1 7   s 1 8   s 2 9   s 3 10  s 4 11        !CH bonds
         s 4 12  s 5 13  s 5 14  s 6 15  s 6 16        !CH bonds
       end
     END
   $END

Note that in this case the $NRTSTR keylist is actually superfluous, because the same two reference structures would be found by default NRT analysis. However, inclusion of the same $NRTSTR keylist for other geometries will insure a consistent 2-reference NRT description over the entire reaction coordinate range, even if the weighting of either structure falls below the default threshold for reference status.

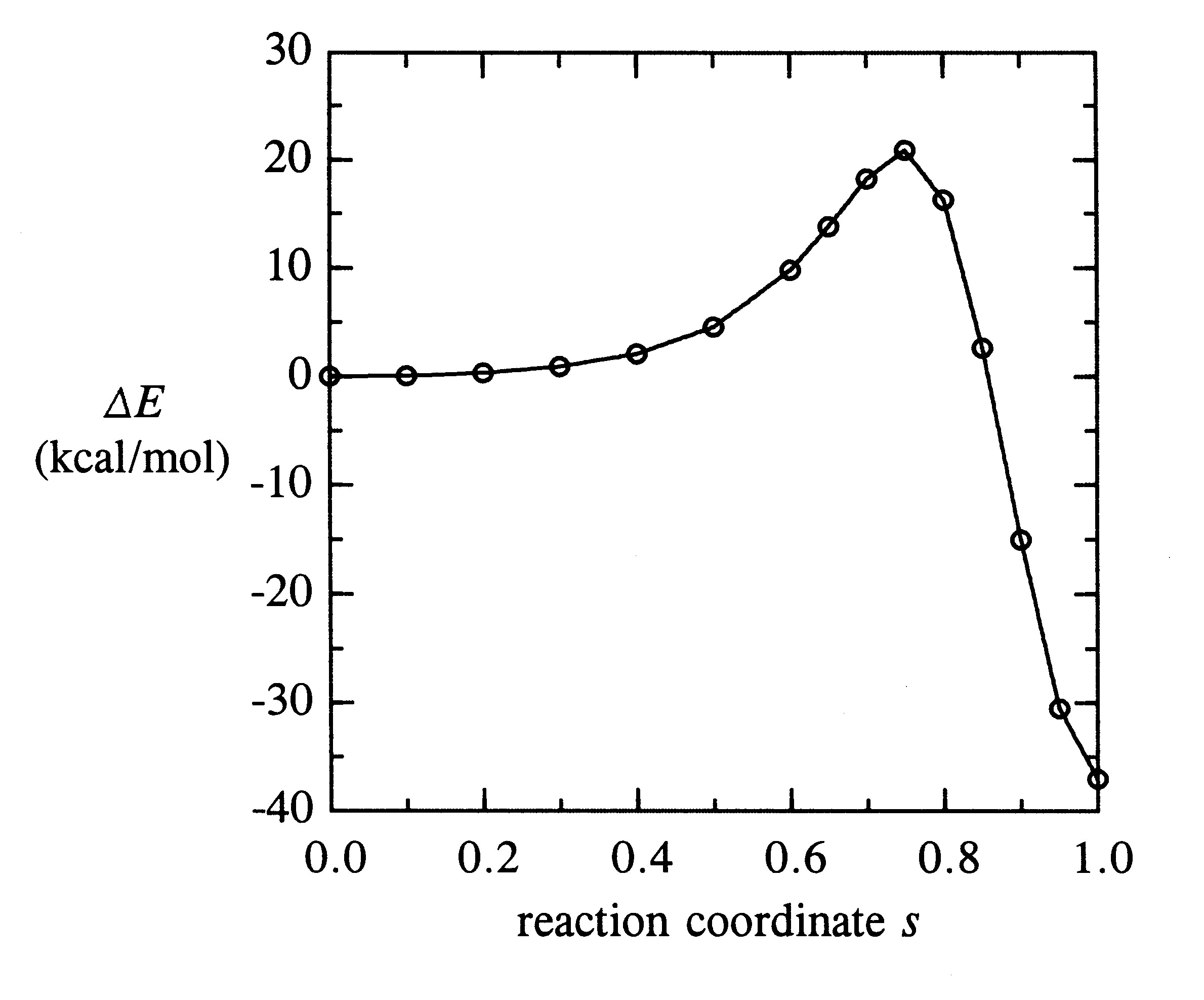
Sample NRT Results Along the Model Diels-Alder Reaction Coordinate

The calculated reaction profile (B3LYP/6-31+G* level) is displayed in the figure below, showing the ca. 20 kcal/mol activation energy barrier and overall -37 kcal/mol exothermicity for this reaction:

The reaction coordinate s is here defined as

s = (dR - d)/(dR - dP)

where d is the distance between the C1-C4 and C5-C6 midpoints, and dR = 4.313 A and dP = 1.419 A are the respective distances in the equilibrium R, P geometry. As defined, s varies continuously from 0 in the weakly bound reactant complex to 1 in the final product, but the reaction profile appears relatively featureless below s ~ 0.5. The TS energy maximum is found to occur at sTS = 0.7508.

The calculated NRT weightings wR, wP of the leading R, P resonance structures are shown below for the region s > 0.5 of greatest variability:

The calculated weightings wR, wP are seen to vary smoothly across the entire profile from the reactant-like (wR >> wP) to the product-like (wP >> wR) region, and their sum accounts for 80-85% of the total NRT weighting at every s value. The natural transition state criterion for the crossing of these two curves (wR = wP) is satisfied near sNTS = 0.76, very similar to the value found from the reaction energy profile.

Finally, the figure below displays the calculated NRT carbon-carbon bond orders bCC along the reaction coordinate.

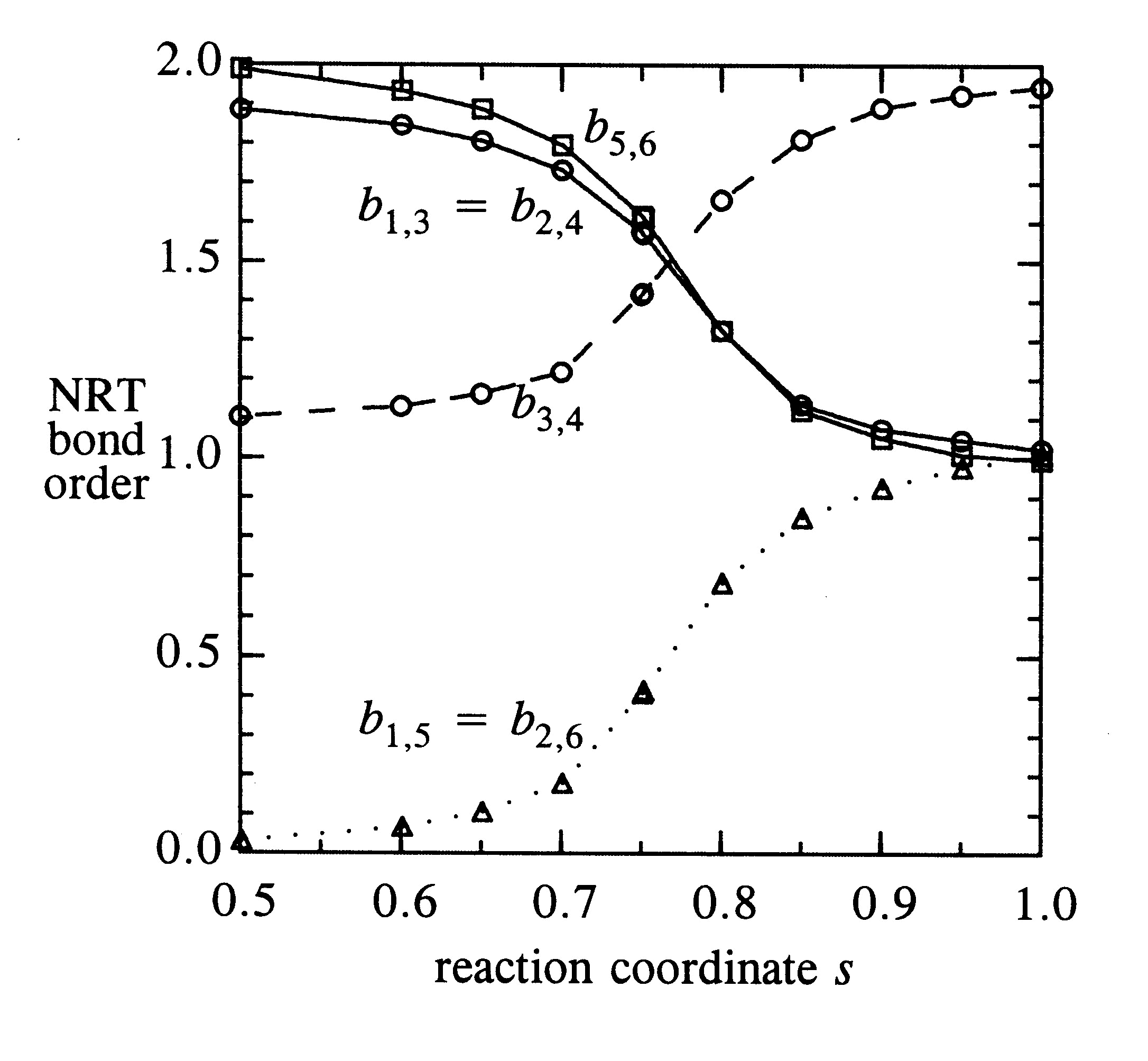Consistent with the expected resonance picture, the C1-C3, C2-C4 bond orders smoothly decrease from double (bCC ~ 2) to single (bCC ~ 1) bond character. The b3,4 bond correspondingly increases from single to double-bond character, while b1,5, b2,6 bond orders simultaneously increase from non-bonded (bCC ~ 0) to single-bonded (bCC ~ 1) character. These bond order switches are all approximately "half-complete" near the transition state, sTS = 0.75. All the calculated NRT weightings and bond orders are seen to vary with s in a continuous and physically reasonable manner.

Transition State Analysis in Convex-Solver NRT

The current QPNRT convex-solver algorithm offers numerous advantages over earlier NBO6-level NRT implementation as described above. In the current NRT implementation,

  • candidate resonance structures are generated in a more general and exhaustive manner, seldom requiring $NRTSTR or other user intervention;
  • all resonance structures are treated at the full "reference structure" level of accuracy; and
  • in contrast to numerical results from previous solvers, the calculated resonance weights and bond orders from the QPNRT convex-solver are provably optimal for satisfying the NRT variational criterion.

    • Thus, the Diels-Alder (or other chosen) reaction can generally be successfully analyzed with resonance structures and bond orders obtained by merely including the "NRT" keyword (without accompanying $NRTSTR keylist or other keyword input) in the input file for each chosen point of the reaction pathway.
    NBO Tutorials
    NBO Home