


This tutorial illustrates how NBOs and MOs are related and offers comparisons of localized (NBO-based) vs. delocalized (MO-based) pictures of the molecular wavefunction for some simple molecular and intermolecular species.
In Part I, we show how to use the CMO keyword and other matrix output keywords to obtain precise mathematical relationships between MOs and NBOs, NLMOs, or other chosen localized orbitals of formamide (NH2CHO), a resonance-delocalized species.
In Part II, we employ the simple methylamine (CH3NH2) species to explore more detailed energetic aspects of analyzing SCF-MO wavefunctions by distinct delocalized vs. localized pathways. The conventional approach employs LCAO-MO mixing diagrams that attempt to picture direct formation of delocalized MO energy levels from AOs or "fragment MOs". The localized VB-like approach proceeds sequentially through hybridization (NHO formation), covalent bonding (NBO formation), and donor-acceptor delocalization (NLMO formation), each having simple and intuitive perturbation-theoretic rationalization. This may be followed (optionally!) by the confusing NLMO → MO canonical transformation that leads to the same final MOs. However, the latter transformation has no physical effect on the SCF-MO wavefunction, energy, or any other observable property and thus may be safely ignored. The resulting gains in conceptual economy show how a localized VB-like perspective can improve understanding of MO-type wavefunctions that are sometimes argued to be in conflict with localized VB-type bonding principles.
In Part III, we employ simple polysulfide chain species to examine various aspects of MO vs. NBO symmetry in intra- and intermolecular interactions. This allows us to see how unphysical aspects of NLMO → MO "delocalization" arise from the characteristic MO dependence on overall angular (rather than local dynamical) symmetry. It also allows comparison of the low-symmetry NBO donor-acceptor approach with conventional HOMO-LUMO analysis as widely employed in the current organic literature.
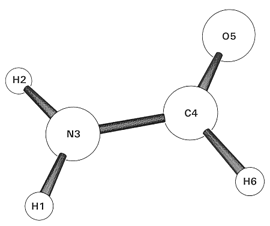
We first consider the elementary formamide species (RHF/3-21G level) as a prototype of resonance-type delocalization. As shown in the sample Gaussian input file, we merely insert the "CMO" ("Canonical Molecular Orbital") keyword into the $NBO keylist, viz.,
$NBO CMO $END
before running the job as usual.
The NBO output for formamide now includes two new tables that quantify the relationship between standard "canonical" MOs and the NBOs of a localized VB-like description of formamide. Both tables are shown in full in the interactive CMO Sample Output listing, with self-explanatory blue-boxes that describe highlighted contents when the mouse-cursor hovers above.
Briefly, the first table gives the NBO composition, showing the leading (>5%) terms of the LCNBO-MO expansion for each occupied or virtual MO. The second table breaks down each MO into contributions of bonding "BD"-type, antibonding "BD*"-type and nonbonding "LP"-type NBOs, showing how contributions of each type are generally found mixed into MOs, whether occupied or virtual. While a few core-type MOs are cleanly related to a single CR-type NBO, most MOs are seen to contain strange mixtures of LP, BD, and BD* type. Moreover, these MO-mixtures are often found to vary dramatically with slight conformational or other geometry changes, whereas NBOs retain highly recognizable and transferable forms. What's going on here?
Let's consider MO12, the highest occupied molecular orbital. As shown in the CMO output, MO12 is approximately expressed in LCNBO-MO form as
composed primarily (57.6% = 0.7592) of the nitrogen lone pair nN NBO, but with substantial contributions from the CO pi-bond (36.2%) and pi*-antibond (6.2%), the former apparently mixed in "antibonding" fashion.
To better understand this strange mixture, we can consider the overall NBO → MO transformation in two distinct steps, viz.,
The successive orbital transformations from NBO (left) to NLMO (center) to final MO (right) are shown below in graphical form:
 |
 |
 |
| NBO | NLMO | MO |
The initial NBO → NLMO transformation is relatively easy to understand; it corresponds to the strong donor-acceptor delocalization of nN (NBO10) with the adjacent π*CO antibond (NBO31), the characteristic allylic-type resonance delocalization that leads to the unusual structural and reactive properties of amide groups (see the NRT keyword sample output for further detail). This accounts for the weaker π*CO mixing term in MO12, which essentially expresses the NLMO composition
in terms of the nN "parent" NBO (90.2%) and its π*CO "delocalization tail" (9.8%).
The final NLMO → MO mixing is more difficult to comprehend in physical terms. Superficially, the strong mixing with πCO appears as a weird "antibonding" (steric repulsion?) with the adjacent filled pi-NBO, seemingly creating a nodal void between nN and πCO regions that are expected to be in conjugation. Fortunately, we can safely ignore the NLMO → MO mixing because it has no effect on the energy or any other observable property of the wavefunction (see discussion of Fock's theorem in the What Are NBOs? link). In effect, the NLMO → MO mixing is an insidious type of "bogus delocalization" that serves to befuddle graphical recognition and suggest ghostly long-range interactions that are physically fictitious. Focussing attention on localized NBO → NLMO donor-acceptor interactions and ignoring superfluous NLMO → MO mixings affords considerable gains in mathematical, graphical, and conceptual simplicity.
How can one obtain further details of NBO → NLMO, NLMO → MO, or overall NBO → MO transformations? In earlier NBO v.4/5, these transformations were obtained with individual "NBONLMO", "NLMOMO", and "NBOMO" keywords, respectively. Although the above keywords are still recognized in NBO 6, these (and many other) transformations can be stipulated as special cases of the MATRIX keyword, with specified initial and final basis parameters in bracket-list format ["MATRIX <initial/final>"], viz.,
An example of the information provided by the "MATRIX <NLMO/MO>" keyword is provided below in Part II.
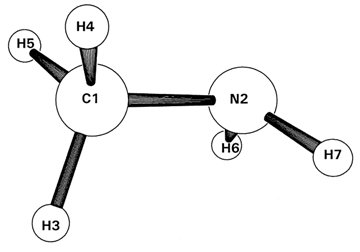
Let's consider further energetic details of how
MOs are envisioned to evolve from conventional AOs (LCAO-MO
description) vs. the
corresponding localized NAO → NHO → NBO → NLMO
→ MO pathway. We employ for this purpose the simple
example of methylamine (CH3NH2, RHF/3-21G
level), which may be considered a typical "well localized"
molecule. (For corresponding description
of MO formation in PtH42-,
see Valency and Bonding, pp. 563-570.)

The figure at the right shows the energy level diagram for valence MOs 3-9 of methylamine in the center, flanked by dotted tie-lines to orbital energy levels of contributing AOs (left) or NAOs (right). Tie-lines are shown for each contributing AO coefficient of magnitude 0.1 or greater, creating a rather dense and confusing mixing pattern for each MO. (Two other AOs of much lower energy, -11.1278 and -15.3613 a.u., also make appreciable contributions to valence MOs, but are omitted here for clarity of the energetically important valence region.)
However, one can see at a glance that contributing NAOs are far fewer in number and span a much smaller energy range (more nearly comparable to that of final MOs) as compared to AOs. Furthermore, the NAOs (unlike AOs) show the proper overall downward trend to form MO levels, as expected on physical grounds. Thus, the conceptual task of making intuitive sense of the mixing patterns seems inherently more complex for the conventional LCAO-MO diagram on the left than for the corresponding LCNAO-MO diagram on the right. The latter forms the starting point for localized NAO → NHO → NBO → NLMO → MO description of MO formation, which we now wish to examine in greater detail.
The first step is formation of directed hybrid NHOs from NAOs, as shown in the orbital energy diagram below for the C (left panel) and H, N atoms (right panel), with dashed tie-lines identifying the most significant contributions to the valence hybrids:

The starting valence NAOs {s,px,py,pz} of C, N show the expected slight breakdown of spherical symmetry in the molecular environment. Nevertheless, one can recognize how these NAOs undergo promotion and hybridization to form directed hybrid NHOs of approximate sp3 character, as expected from the standard theory of equivalent hybrid formation (see, e.g., V&B, p. 105ff). As anticipated by Bent's rule (V&B, p. 138ff), the detailed NAO → NHO mixing coefficients show slightly increased p-character directed toward more electronegative ligands, leading to the slight hybrid inequivalencies required on physical grounds. As seen in the diagram, the energetic center of gravity of final NHOs lies somewhat above the starting NAOs, reflecting the orbital "promotion" required to achieve effective directional bonding. For the five H atoms, the "hybrid" NHOs are essentially identical to the starting 1sH NAOs, with orbital energies slightly separated into (1,2,2) splitting pattern by the asymmetric molecular environment.
The second step is covalent bonding of directional hybrid NHOs to form the Lewis-type NBOs of the skeletal bonding framework, as depicted in the energy diagram below:

As shown in the diagram, the nonbonding nitrogen lone pair nN is merely a "spectator", carried over from the NAO → NHO diagram, whereas remaining NHOs pair up in the expected manner to form the covalent σCH, σNH, σCN NBOs of the formal Lewis structure. Each NBO is seen to be strongly stabilized in energy compared to its parent NHOs (as can be readily understood from the elementary theory of chemical covalency; see V&B, p. 91ff), leading to the overall energetic lowering that provides the essential reward for molecule formation. Filling each valence NBO with two electrons (together with the C, N core NBOs, which lie far below the energy range of the diagram) gives the elementary "Natural Lewis Structure" (NLS) representation of the molecule, corresponding to the familiar Lewis dot-diagram of freshman chemistry.
The final step is delocalization ("resonance mixing") from the idealized NLS form, in which each localized Lewis-type NBO is replaced by its associated semi-localized NLMO, as shown in the left-half of diagram below:
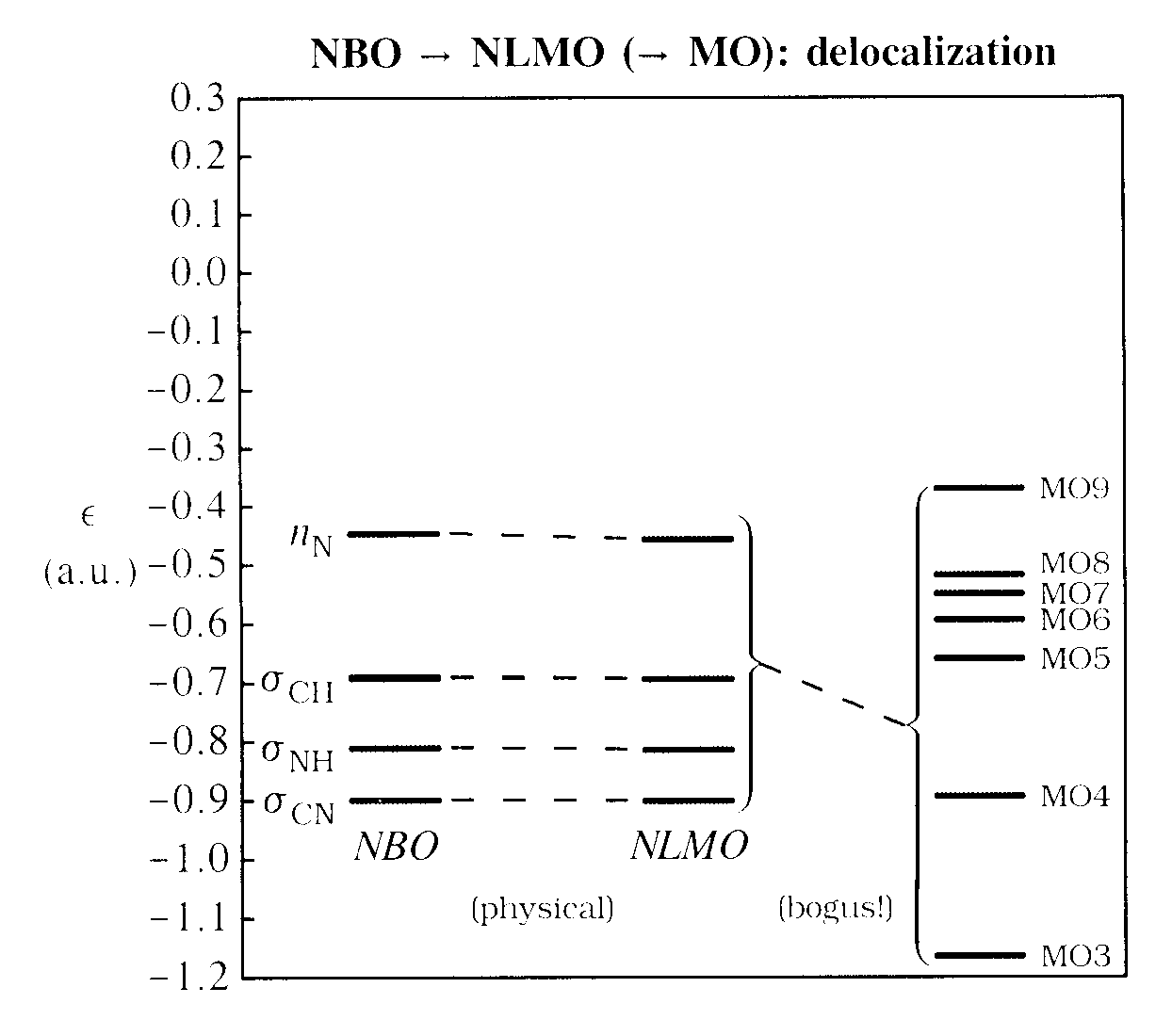
Each such delocalization is intrinsically stabilizing (see, e.g., V&B, p. 19ff, 182ff, 263ff). However, in this case the delocalization tails of the NLMOs (primarily into antiperiplanar vicinal antibonds; see V&B, p. 240ff) are rather weak, corresponding to downward shifts in NLMO orbital energies that are nearly imperceptible on the energy scale of the diagram. These slight NBO → NLMO energy shifts represent the only physically significant "delocalization effects" in methylamine, consistent with its usual formulation as a "well localized" molecule. In contrast, the bewilderingly complex NLMO → MO mixings depicted at the right of the diagram are appropriately labelled as "bogus", because they correspond to no physical effect on total energy, electron density or other observable property.
Focussing on the physically meaningful NAO → NHO → NBO → NLMO steps, while ignoring the superfluous NLMO → MO step, brings considerable simplification to chemical wavefunction analysis. If desired, however, the ghostly mixings of MOs can be further investigated with keywords such as CMO (from NBOs to MOs) or NLMOMO (from NLMOs to MOs). For example, the portions of the "MOs in the NLMO basis" transformation matrix that relate the 7 highest-energy (valence Lewis-type) NLMOs to the corresponding highest-occupied MOs 3-9 are tabulated below:
MOs in the NLMO basis:
MO3 MO4 MO5 MO6 MO7 MO8 MO9
------- ------- ------- ------- ------- ------- -------
NLMO C 1- N 2 0.6293 0.1244 0.0000 0.3240 0.6817 0.0000 -0.1061
NLMO C 1- H 3 0.2062 0.4717 0.0000 -0.7749 0.1388 0.0000 0.3345
NLMO C 1- H 4 0.1838 0.4914 0.3818 0.2308 -0.3925 0.5952 -0.1187
NLMO C 1- H 5 0.1838 0.4914 -0.3818 0.2308 -0.3925 -0.5952 -0.1187
NLMO N 2- H 6 0.4743 -0.3566 -0.5952 -0.1961 -0.3035 0.3818 -0.1183
NLMO N 2- H 7 0.4743 -0.3566 0.5952 -0.1961 -0.3035 -0.3818 -0.1183
NLMO N 2(lp) 0.1677 -0.1230 0.0000 0.3331 -0.1536 0.0000 0.9057
In contrast to the near-diagonal character of the NBO → NLMO transformation (which expresses the only physically relevant delocalization), the NLMO → MO transformation matrix contains large off-diagonal mixing coefficients involving virtually all NLMOs. Moreover, such NLMO-MO mixing coefficients are found to vary with alterations of geometry or other physical changes, thus appearing to harbor information concerning interactions of physical significance. However, such illusory "physical variability" merely adds to the insidious and unphysical character of NLMO → MO "delocalization", which should play no substantive role in conceptual analysis of SCF-MO wavefunctions.
Conflicting concepts of delocalization can often be traced to the disparate role of symmetry in MO vs. NBO theory. As is well known, localized Lewis-type bonding patterns are often of lower symmetry than the molecular point group (as, e.g., for either Kekulé structure of D6h benzene). Such "symmetry breaking" is sometimes considered to be a defect of NBO theory, as compared to MO theory where conservation of molecular symmetry is paramount. (Indeed, many beginning students are led into thinking that "quantum chemistry" involves little more than reading MO coefficients from character tables!) In the present section we employ simple model hydrogen thioperoxide (HSSH) and related polysulfide chain species to examine various aspects of MO vs. NBO symmetry in intra- and intermolecular interactions.
Because canonical MOs are defined as eigenfunctions of the Fock operator, which exhibits the full symmetry of the nuclear point group, they necessarily form a basis for irreducible representations of full point-group symmetry. (In contrast, localized bonds often provide only a reducible representation of molecular symmetry.) The NBOs typically exhibit the effective local symmetry of the bonding environment, such as the effective C2v symmetry of ether-type X-O-X or carbonyl-type X2C=O linkages that lead to characteristic σ/π character of oxygen lone pairs.
Practically speaking, the strict irreducible symmetry character of MOs is less significant or advantageous than may appear. Beyond triatomic species (which perforce have a plane of symmetry), exact point-group symmetry other than trivial C1 is found only at isolated equilibrium points of the potential energy surface, and even infinitesimal vibrational departures destroy presumed "exact" symmetry of the nuclear framework. In addition, numerical MOs calculated with finite arithmetic precision often fail to exhibit the expected ideal point-group symmetry, even if nuclear symmetry is maintained exactly. Paradoxically, such loss of exact symmetry may lead to gains in physical insight by removing unphysical mixings involving unrealistically large separations or weak couplings, as illustrated below in valence and core MOs of model polysulfide chain species.
Gaussian input is shown below for HSSH in calculated C2-symmetric equilibrium geometry at B3LYP/3-21G level:
#b3lyp/3-21g pop=nboread HSSH 0 1 H S 1 1.3787 S 2 2.2940 1 95.84 H 3 1.3787 2 95.84 1 94.70 $NBO file=hssh_eq cmo nlmomo $END
(Of course, accurate description of such species requires higher basis levels, but model 3-21G treatment adequately illustrates qualitative symmetry properties found in more accurate MOs.)
As shown in CMO analysis output below for selected occupied and virtual MOs 1, 2, 16-20, the default symmetry-adapted MOs all show the expected mixing patterns between symmetry-equivalent atoms, which apparently depict "strong delocalization" between H'S' and H"S" ends of the molecule:
CMO: NBO Analysis of Canonical Molecular Orbitals
Leading (> 5%) NBO Contributions to Molecular Orbitals
======================================================
MO 1 (occ): orbital energy = -88.279400 a.u.
0.707*[ 4]: CR ( 1) S 2(cr)
0.707*[ 9]: CR ( 1) S 3(cr)
MO 2 (occ): orbital energy = -88.279359 a.u.
0.707*[ 4]: CR ( 1) S 2(cr)
-0.707*[ 9]: CR ( 1) S 3(cr)
...
MO 16 (occ): orbital energy = -0.278299 a.u.
0.665*[ 15]: LP ( 2) S 2(lp)
0.665*[ 17]: LP ( 2) S 3(lp)
MO 17 (occ): orbital energy = -0.272831 a.u.
-0.694*[ 15]: LP ( 2) S 2(lp)
0.694*[ 17]: LP ( 2) S 3(lp)
MO 18 (vir): orbital energy = -0.104557 a.u.
0.990*[ 29]: BD*( 1) S 2- S 3*
MO 19 (vir): orbital energy = 0.024476 a.u.
0.658*[ 30]: BD*( 1) S 3- H 4*
0.658*[ 28]: BD*( 1) H 1- S 2*
MO 20 (vir): orbital energy = 0.027461 a.u.
-0.661*[ 30]: BD*( 1) S 3- H 4*
0.661*[ 28]: BD*( 1) H 1- S 2*
Somewhat counterintuitively from a chemical viewpoint, this supposed "delocalization" is seen to extend to the deep inner core 1s levels MO1 and MO2, which appear respectively as in-phase or out-of-phase mixtures of corresponding CR-type NBOs, viz.,
Because the formal group theory is independent of physical distances, the same result must follow (if the numerical calculations were exact) whether the RS'S" separation is 2.29 Å or 2.29 light-years! However, such inter-galactic delocalization of core electrons is wholly implausible on chemical grounds. While similar artifacts affect higher valence MOs, we focus here on the deeply buried core 1s orbitals where the unphysical aspects of NLMO → MO symmetry delocalization are most easily seen.
The fictitious character of symmetry-induced core delocalization can be illustrated more directly in long-chain polysulfides HSnH of extended (all-anti) form, which alternate between C2h or C2v symmetry for even or odd n. In the odd-n C2v species, the unique central S atom is found to have a sensibly localized core 1s MO, whereas those for remote terminal S′, S″ atoms have strongly mixed forms, similar to MO1, MO2 above. Each such strongly mixed S', S" core pair appears strangely oblivious to comparable "delocalizations" with the many nearby cores that separate the pair.
Mercifully, the symmetry-imposed core-core mixing patterns are usually truncated at some finite cutoff distance RS'S", due to the limited numerical precision of machine computations. We can illustrate such "spontaneous symmetry-breaking" in terms of the increasing asymmetry between symmetry-matched S', S" core levels as n increases. For this purpose we employ idealized Pople-Gordon geometry for odd-n HSnH species of C2v symmetry, as illustrated in the sample Gaussian input file below for n = 3, with "nosymm" keyword to prevent default imposition of formal group-theoretic mixing:

#b3lyp/3-21g pop=nboread nosymm HSSSH Pople-Gordon C2v 0 1 H S 1 1.3400 S 2 2.0800 1 109.4712 S 3 2.0800 2 109.4712 1 180.0000 H 4 1.3400 3 109.4712 2 180.0000 $NBO file=hs3h cmo nlmomo $END
For n = 7, for example, the curious localization patterns for low-lying core-type MOs are illustrated in the orbital amplitude profiles below, showing orbital amplitude profiles along the chain of sulfur atoms. The panels contrast the completely localized form of φ1 ["spiked" only at S(4)] with the "delocalized" φ2 [spiked symmetrically between S(3), S(5)], φ6 [spiked slightly unsymmetrically between S(2), S(6)], and φ6 (spiked more unsymmetrically between S(1), S(7)]:
The plot below shows the calculated percentage asymmetry (%-asym.) of symmetry-paired S', S" core MOs (1,n), (2,n-1) and (3,n-2), up to n = 11, obtained as the difference between cS', cS" contributions in CMO output:
As shown in the plot, formal group-theoretic symmetry patterns are found to be broken even at n = 3, and numerical asymmetries continue to grow erratically until predominantly localized character is found for symmetry-pairs separated by more than about four atoms. The erratic, discontinuous behavior of the apparent MO "localization transition" betrays its unphysical character, as does the absence of corresponding changes in total energy, charge distribution, or other observable properties. Similar artifacts affect higher valence-level MOs as RS'S" increases.
The in-phase or out-of-phase mixing coefficients of MOs are often used to infer their individual contributions to physical "bonding" or "antibonding" between atoms. However, such inferences can be quite superficial and misleading, as shown below in the second section of CMO output for occupied MOs 1-17 of HSSH:
Molecular Orbital Atom-Atom Bonding Character
================================================
bonding nonbonding antibonding
MO (2c, 3c) (1c, 1c*) (2c*, 3c*)
------ --------------- ---------- ---------------
1(o) 0.500 S 3
0.500 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
2(o) 0.500 S 3
0.500 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
3(o) 0.488 S 3
0.488 S 2
_____ _____ _____
0.004(b) 0.996(n) 0.000(a) total
--------------------------------------------------------
4(o) 0.485 S 3
0.485 S 2
_____ _____ _____
0.008(b) 0.992(n) 0.000(a) total
--------------------------------------------------------
5(o) 0.440 S 3
0.440 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
6(o) 0.432 S 3
0.432 S 2
_____ _____ _____
0.001(b) 0.999(n) 0.000(a) total
--------------------------------------------------------
7(o) 0.499 S 3
0.499 S 2
_____ _____ _____
0.001(b) 0.999(n) 0.000(a) total
--------------------------------------------------------
8(o) 0.500 S 3
0.500 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
9(o) 0.500 S 3
0.500 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
10(o) 0.500 S 3
0.500 S 2
_____ _____ _____
0.000(b) 1.000(n) 0.000(a) total
--------------------------------------------------------
11(o) 0.192 S 2- S 3 0.239 S 3
0.150 S 3- H 4 0.239 S 2
0.150 H 1- S 2
_____ _____ _____
0.492(b) 0.508(n) 0.000(a) total
--------------------------------------------------------
12(o) 0.234 S 3- H 4 0.253 S 3
0.234 H 1- S 2 0.253 S 2
_____ _____ _____
0.467(b) 0.532(n) 0.001(a) total
--------------------------------------------------------
13(o) 0.311 S 3- H 4
0.311 H 1- S 2
0.279 S 2- S 3
_____ _____ _____
0.901(b) 0.099(n) 0.000(a) total
--------------------------------------------------------
14(o) 0.250 S 3- H 4 0.234 S 3
0.250 H 1- S 2 0.234 S 2
_____ _____ _____
0.499(b) 0.500(n) 0.001(a) total
--------------------------------------------------------
15(o) 0.507 S 2- S 3 0.178 S 3
0.178 S 2
_____ _____ _____
0.552(b) 0.446(n) 0.002(a) total
--------------------------------------------------------
16(o) 0.442 S 3
0.442 S 2
_____ _____ _____
0.044(b) 0.953(n) 0.004(a) total
--------------------------------------------------------
17(o) 0.482 S 3
0.482 S 2
_____ _____ _____
0.027(b) 0.969(n) 0.004(a) total
--------------------------------------------------------
According to their NBO composition, all low-lying MOs 1-10 associated with low-lying 1s,2s,2p sulfur core orbitals are found to be essentially 100% nonbonding in character, consistent with chemical evidence. Significant "antibonding" character is also absent in higher occupied MOs, and predominant "bonding" character appears only in MO 13 (90%), with lesser contributions from MOs 11 (51%), 12 (53%), 14 (50%) and 15 (55%) which sum to the expected total bond order (3) of the Lewis diagram. In this respect as well, the florid MO mixing patterns prove to be largely illusory.
We can conclude that symmetry-induced MO mixing patterns belong primarily to the NLMO → MO domain of "bogus" delocalization. Rather than an advantage of the MO approach, these mixing patterns serve largely to distract attention from the physically relevant NBO → NLMO delocalization patterns that reflect the effective local symmetry of the bonding environment.
Let's look next at some details of the "frontier" orbitals of HSSH, comparing the localized donor and acceptor NBOs with the corresponding highest occupied (HOMO) and lowest unoccupied (LUMO) MOs that are widely believed to control intermolecular interactions. As a simple example of such interactions, we consider formation of the dimer complex
which leads to the doubly hydrogen-bonded structure and associated Gaussian z-matrix file shown below:

#b3lyp/3-21g pop=nboread (HSSH)2, E = -1587.2801307 0 1 H 0.561174 1.298693 -0.067032 S 1.945207 1.172562 -0.083642 S 1.926593 -1.125691 0.002377 H 2.049909 -1.223986 1.371401 H -0.559670 -1.296040 -0.078236 S -1.944460 -1.172031 -0.083195 S -1.927463 1.125016 0.002123 H -2.049447 1.223627 1.371254 $nbo file=hssh_2 cmo nlmomo $end
The NBO donor-acceptor picture is rather straightforward. Consistent with innumerable other H-bonded species (see V&B Sec. 5.2), each H-bond is expected to originate in a localized n-σ* donor-acceptor interaction, in this case of nS → σ*SH form. From the localized perspective, the relevant "frontier orbitals" are the π-type nS lone pair (donor) and the σ*SH antibond (acceptor) NBO on each SH moiety, as shown in the diagrams below. Each is expected to participate in complementary nS' → σ*S"H" intermolecular delocalization interactions with NBOs of the other monomer, leading to an associated NLMO of weakly delocalized form for each resulting H-bond.
When two such HSSH monomers come into proximity, their donor and acceptor NBOs are able to pair up "hand in glove" in a cyclic conjugative arrangement to form the two complementary S···H-S hydrogen bonds of the equilibrium dimer structure, each with favorable near-linear nS'-σ*S"H" geometry. The NBOView images below display one of these two H-bonds in terms of the associated NBO donor-acceptor overlap diagram (left) and slightly delocalized NLMO (right). The latter is found (from NBONLMO output) to have the numerical form
As shown in the diagram, the final NLMO is only weakly perturbed from the form of its parent nS' donor NBO, due to weak (~1.9%) intermolecular delocalization into the neighboring σ*S"H" acceptor NBO. The high NBO or NLMO transferability from monomer to dimer is evident.
The corresponding delocalized "HOMO-LUMO picture" is far less straightforward. As shown in the first section of CMO output above, and illustrated in orbital diagrams below, the HOMO (MO17) is found to be the "antibonding mixture" of π-type nS', nS" NBOs on each monomer, viz.,
The LUMO is essentially a pure NBO, the localized σ*S'S" antibond between the two sulfur atoms,
but (as shown below) it plays no significant role in complex formation.
Neither monomer MO seems particularly useful in suggesting structural features of the dimer complex, and neither transfers recognizably into the dimer framework. However, if we consider in addition the second occupied (SOMO) MO17, the "bonding" counterpart of MO18,
we can recover the relevant donor NBOs as the "HOMO + SOMO" and "HOMO - SOMO" linear combinations which "undo" the symmetry-imposed mixing, viz.,
The LUMO bears no discernible relationship to structural features of the dimer complex, nor to the localized NBO acceptor σ*S'H'. To recover the latter, we must look instead to the second unoccupied (SUMO) MO19 and third unoccupied (TUMO) MO20, which are of the approximate form
These symmetry mixtures can again be "undone" to give "SUMO + TUMO" and "SUMO - TUMO" combinations that recover the two localized hydride antibond NBOs,
However, only one of these two antibonds participates significantly in H-bonding, while the other, essentially unperturbed, protrudes in a perpendicular direction. Hence, only "half" of SUMO and TUMO contribute usefully to dimer interaction. Although one could pursue such logic to re-formulate aspects of the localized nS' → σ*S"H" picture as a corresponding MO-based "(HOMO & SOMO)-(SUMO & TUMO) picture", there seems little conceptual incentive to pursue this tortured alternative.
[In the foregoing qualitative discussion of symmetry issues, we have attempted to draw the tightest possible connection between NBOs and MOs by neglecting the weak σ*SH contributions to occupied nS-type NLMOs arising from intramolecular hyperconjugative interactions (see V&B, Sec. 3.4). However, we should recall that these weak contributions to electron density are what fundamentally distinguish "non-Lewis NBOs" from "virtual MOs". The latter, by definition, have zero occupancy and make no contribution to the total MO wavefunction, electron density, or other observable property, whereas the former generally have non-zero occupancies and contribute irreducibly to all system properties, both in correlated and uncorrelated levels of theory.]
We can conclude that due to their tight adaptaption to the symmetry of the starting monomer, HOMO and LUMO orbitals are unlikely to correctly suggest intermolecular donor-acceptor structural features, unless the complexation path or product symmetry coincides with starting monomer symmetry. Use of NBOs eliminates the need to first "undo" spurious HOMO/LUMO symmetry mixings in order to identify the physically relevant orbitals. In this respect, NBOs again prove advantageous over MOs for their flexibility, transferability and conceptual economy.